How To Find The Domain And Range Of Each Relation
Earlier learning about Domain and Range of a Relation firstly know what Relations are. A relation is a rule that relates an chemical element from one set to the other set up. Consider two non-empty sets A and B then the relation is a subset of Cartesian Product AxB.
The domain is the ready of all first elements of the ordered pairs. The range on the other manus is the set up of all second elements of the ordered pairs. Nevertheless, Range includes only the elements used by the function. There lies in a trick in the range i.eastward. Prepare B can be equal to the range of relation or bigger than that. This is because in that location can exist elements in Set B that aren't related to Set up A.
- Relations and Mapping
- Ordered Pair
- Cartesian Production of Two Sets
- Relation in Math
- Practice Test on Math Relation
- Functions or Mapping
- Domain Co-domain and Range of Office
- Math Practice Examination on Functions
Domain and Range Definition
If R be a relation from Set A to Set up B then the Set of beginning elements belonging to the ordered pair is called the Domain of R. We can represent the Domain every bit such
Dom(R) = {a ∈ A: (a, b) ∈ R for some b ∈ B}
The Set up of Second Components belonging to the ordered pair is chosen the Range of R. It tin be denoted as follows
R = {b ∈ B: (a, b) ∈R for some a ∈ A}
Thus, Domain and Range are given by Domain (R) = {a : (a, b) ∈ R} and Range (R) = {b : (a, b) ∈ R}.
Solved Examples on Domain and Range of a Relation
1. State the domain and range of the following relation: (centre color, student'southward proper name).
A = {(blueish, John), (green, William), (dark-brown,Wilson), (blue, Moy), (brown, Abraham), (green, Dutt)}. State whether the relation is a office?
Solution:
Domain: {blue, greenish, brown} Range: {John, William, Wilson, Moy, Abraham, Dutt}
No, the relation is not a function since the eye colors are repeated.
2. State the domain and range of the following relation: {(iv,iii), (-i,7), (ii,-3), (7,v), (six,-2)}?
Solution:
The domain is the first component of the ordered pairs. Whereas, Range is the 2d Component of the ordered pairs. Remove the duplicates if any are present.
Domain = {four, -i, two, 7, six} Range = {3, 7, -3, 5, -ii}
3. From the following Pointer Diagram find the Domain and Range and depict the relation betwixt them?
Solution:
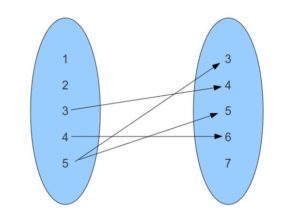
Domain = {iii, iv, 5}
Range = {3, 4, v, 6}
R = {(3, 4), (four, half-dozen), (5, iii), (5, 5)}
4. Determine the domain and range of the relation R defined by
R = {x – 2, 2x + 3} : ten ∈ {0, one, 2, iii, 4, 5}
Solution:
Given x = {0, 1, 2, 3, 4, 5}
ten = 0 ⇒ 10 – 2 = 0 – two = -2 and 2x + three = 2*0 + 3 = 3
10 = 1 ⇒ x-two = 1-ii = -1 and 2x+iii = 2*ane+three = v
x = 2 ⇒ ten-2 = ii-2 = 0 and 2x+3 = 2*two+three = 7
ten = 3 ⇒ x-two = 3-ii = ane advertizing 2x+3 = two*3+3 = 9
x = 4 ⇒ ten-2 = four-2 = 2 and 2x+3 = 2*four+3 = 11
x = 5 ⇒ x-ii = 5-ii =3 and 2x+3 = 2*5+3 = thirteen
Hence R = {-ii, 3), (-one, 5), (0, 7), (1, 9), (2, 11), (three, thirteen)
Domain of R = {-2, -1, 0, ane, ii, 3}
Range of R = {3, 5, 7, 9, 11, 13}
5. The beneath figure shows a relation between Set x and Prepare y. Write the same in Roster Class, Set up Builder Form, and observe the domain and Range?
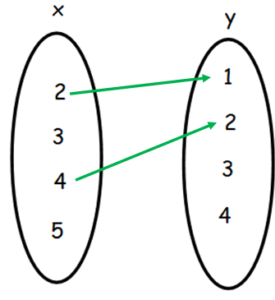
Solution:
In the Set Builder Course R = {(ten, y): x is the square of y, x ∈ X, y ∈ Y}
In Roster Form R = {(2, 1)(four, ii)}
Domain = {2, 4}
Range = {1, 2}
6. The Arrow Diagram Shows the Relation R from Set C to Set up D. Write the relation R in Roster Form?
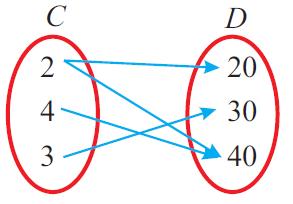
Solution:
We observe the relation R using the Pointer Diagram To a higher place
From that Relation R in Roster Form = {(2,twenty) ; (2, twoscore) ; (four, 40) ; (3, 30)}
How To Find The Domain And Range Of Each Relation,
Source: https://www.learncbse.in/domain-and-range-of-a-relation/
Posted by: morriswhoppy.blogspot.com


0 Response to "How To Find The Domain And Range Of Each Relation"
Post a Comment